REVISION DATE: 11-Feb-2013 14:02:03
So Mike redid the linearity data. In this setup Mike used a sphere which allowed the use of a bare fiber "Lu" collector, which has a much larger responsivity than Es. This allows higher light levels and shorted integration times (~ 1 sec). He also took 2dk/5lt/2k giving us more stable data. THis data set looks really nice! Very clean. I processed the data the same way I did the previous linearity data. Below is the description of the process used to calculate the linearity for this data set.
Using Carol's linearity write up and after talking to Carol to make sure I understood I started setting up the matrices to do solve the linear equations. Also reading the Saunders and Shumaker (1984) paper is helpful. I will decribe below the way I set up the matrices and my understanding of how it works. You should be able to follow along using Carol write-up.
PDF papers on linearity:
GS5000-14_manual_2.pdf
Linearity of FISH-1.pdf
met8_2_009.pdf
saunders_shumaker_beamconjoiner_AO_23.pdf
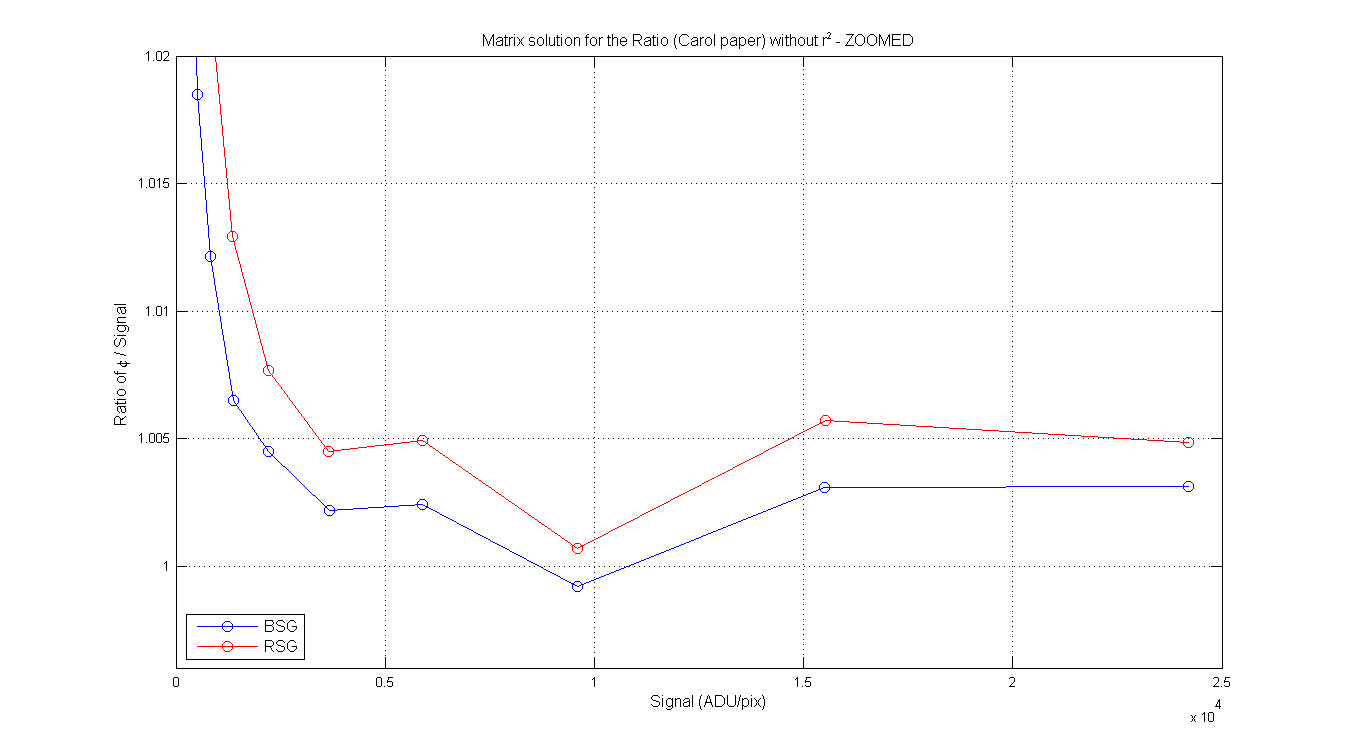
BSG/RSG Table from Carols write-up page 2-3. Column 2 is the RD or S (mean of pixeles around max), column 3 is the φ from the matrix math, column 4 is the residual from Carols paper and Colum 5 is the ratio of φ / signal. Same for the RSG. Each of the columns contains the φ, Residual and ratio with and without the r² in the equations.
r coefficents with r²
BSG r values = [ -7.6534 2.2471e-007 ]
RSG r values = [ -7.099 3.4753e-007 ]
r coefficents without r²
BSG r values = [ 15.4471 ]
RSG r values = [ 28.9707 ]
| BSG | RSG | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Aperature | RD or S /%std | φ (w r² / wo r²) | Residual-Y (w r² / wo r²) | Ratio (w r² / wo r²) | Aperature | RD or S / %std | φ (w r² / wo r²) | Residual-Y (w r² / wo r²) | Ratio (w r² / wo r²) |
| A | 36.796/ 7.621 | 30.994/ 47.710 | 1.851/ -4.533 | 0.842/ 1.297 | A | 35.988/ 5.635 | 30.769/ 56.870 | 1.880/ -8.089 | 0.855/ 1.580 |
| IA | 70.097/ 4.231 | -1.853/ 4.533 | IA | 69.712/ 3.347 | -1.884/ 8.089 | ||||
| I | 34.195/ 8.448 | 29.598/ 42.368 | 3.056/ -7.274 | 0.866/ 1.239 | I | 34.517/ 6.106 | 29.961/ 49.901 | 2.542/ -13.587 | 0.868/ 1.446 |
| IB | 110.984/ 3.135 | -1.211/ 2.740 | IB | 110.645/ 2.308 | -0.671/ 5.498 | ||||
| B | 77.209/ 4.002 | 72.524/ 86.803 | 2.967/ -5.853 | 0.939/ 1.124 | B | 77.308/ 3.060 | 72.917/ 95.212 | 2.706/ -11.066 | 0.943/ 1.232 |
| JB | 191.293/ 1.833 | -1.781/ 3.113 | JB | 191.194/ 1.463 | -2.073/ 5.568 | ||||
| J | 113.909/ 2.721 | 109.343/ 123.050 | 3.084/ -6.306 | 0.960/ 1.080 | J | 113.156/ 1.999 | 109.117/ 130.520 | 3.056/ -11.606 | 0.964/ 1.153 |
| JC | 313.393/ 1.452 | -1.369/ 3.193 | JC | 311.327/ 1.019 | -1.085/ 6.038 | ||||
| C | 199.997/ 1.586 | 195.050/ 208.983 | 2.697/ -6.461 | 0.975/ 1.045 | C | 198.660/ 1.371 | 194.060/ 215.816 | 2.485/ -11.815 | 0.977/ 1.086 |
| KC | 513.398/ 1.268 | -1.508/ 3.268 | KC | 512.079/ 0.874 | -1.678/ 5.776 | ||||
| K | 314.101/ 1.421 | 309.247/ 323.130 | 2.777/ -6.418 | 0.985/ 1.029 | K | 313.581/ 1.013 | 309.333/ 331.010 | 2.817/ -11.542 | 0.986/ 1.056 |
| KD | 834.674/ 1.161 | -1.745/ 3.150 | KD | 830.536/ 0.659 | -1.869/ 5.765 | ||||
| D | 520.518/ 1.278 | 516.185/ 530.141 | 3.260/ -5.824 | 0.992/ 1.018 | D | 515.962/ 0.733 | 512.474/ 534.262 | 3.518/ -10.671 | 0.993/ 1.035 |
| LD | 1347.366/ 0.964 | -2.765/ 2.674 | LD | 1343.419/ 0.464 | -3.568/ 4.906 | ||||
| L | 825.333/ 1.221 | 821.170/ 835.345 | 3.338/ -5.434 | 0.995/ 1.012 | L | 824.946/ 0.626 | 820.906/ 843.035 | 2.823/ -10.882 | 0.995/ 1.022 |
| LE | 2192.315/ 0.978 | -3.854/ 2.760 | LE | 2185.691/ 0.356 | -4.303/ 5.976 | ||||
| E | 1366.292/ 1.029 | 1360.717/1375.177 | 1.659/ -6.562 | 0.996/ 1.007 | E | 1360.003/ 0.475 | 1355.043/1377.602 | 1.496/ -11.372 | 0.996/ 1.013 |
| ME | 3587.785/ 0.978 | -6.589/ 3.802 | ME | 3581.088/ 0.340 | -10.712/ 5.396 | ||||
| M | 2221.907/ 0.965 | 2215.719/2231.858 | 0.356/ -5.496 | 0.997/ 1.004 | M | 2220.851/ 0.403 | 2212.691/2237.852 | -2.775/ -11.970 | 0.996/ 1.008 |
| MF | 5888.926/ 0.927 | -17.357/ 1.694 | MF | 5872.737/ 0.287 | -22.827/ 6.574 | ||||
| F | 3666.225/ 0.956 | 3655.990/3674.209 | -5.603/ -7.463 | 0.997/ 1.002 | F | 3653.968/ 0.361 | 3642.107/3670.430 | -9.402/ -12.508 | 0.997/ 1.005 |
| NF | 9558.468/ 0.937 | -39.728/ 5.769 | NF | 9554.364/ 0.271 | -64.472/ 5.934 | ||||
| N | 5891.186/ 0.931 | 5875.627/5905.474 | -15.705/ -1.159 | 0.997/ 1.002 | N | 5889.815/ 0.316 | 5872.410/5918.839 | -22.361/ 0.054 | 0.997/ 1.005 |
| NG | 15492.408/ 0.919 | -109.095/ -4.610 | NG | 15486.570/ 0.263 | -167.424/ -5.988 | ||||
| G | 9605.580/ 0.939 | 9553.966/9597.771 | -64.694/ -23.256 | 0.995/ 0.999 | G | 9584.196/ 0.266 | 9522.985/9590.714 | -86.035/ -22.453 | 0.994/ 1.001 |
| OG | 25090.939/ 0.936 | -258.485/ 27.866 | OG | 25136.470/ 0.239 | -416.247/ 28.441 | ||||
| O | 15488.946/ 0.936 | 15412.303/15536.481 | -122.900/ 32.087 | 0.995/ 1.003 | O | 15514.664/ 0.258 | 15409.721/15603.168 | -181.496/ 59.533 | 0.993/ 1.006 |
| OH | 39852.884/ 0.915 | -723.174/ -59.954 | OH | 39980.108/ 0.240 | -1119.704/ -87.974 | ||||
| H | 24196.496/ 0.993 | 24066.654/24271.897 | -253.751/ 59.954 | 0.995/ 1.003 | H | 24200.993/ 0.446 | 23999.075/24317.937 | -398.361/ 87.974 | 0.992/ 1.005 |
Figure 1
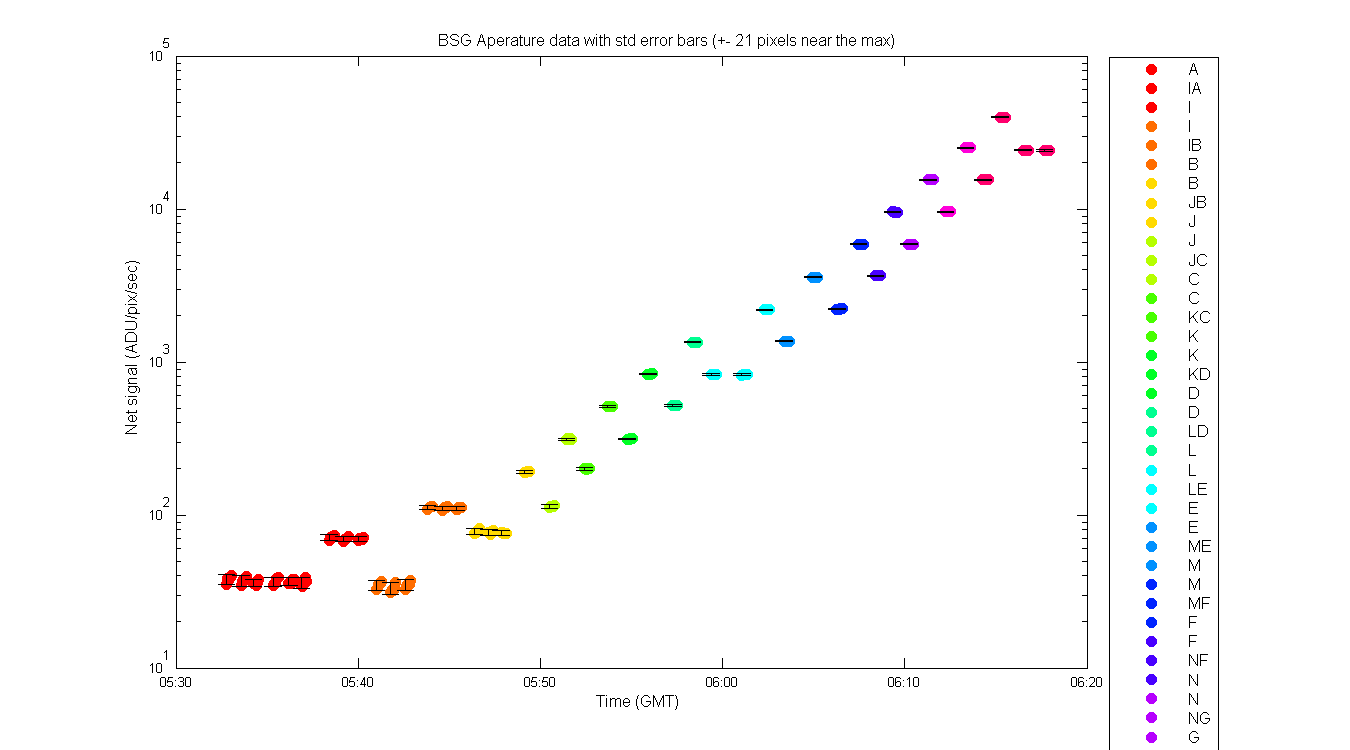
Figure 2
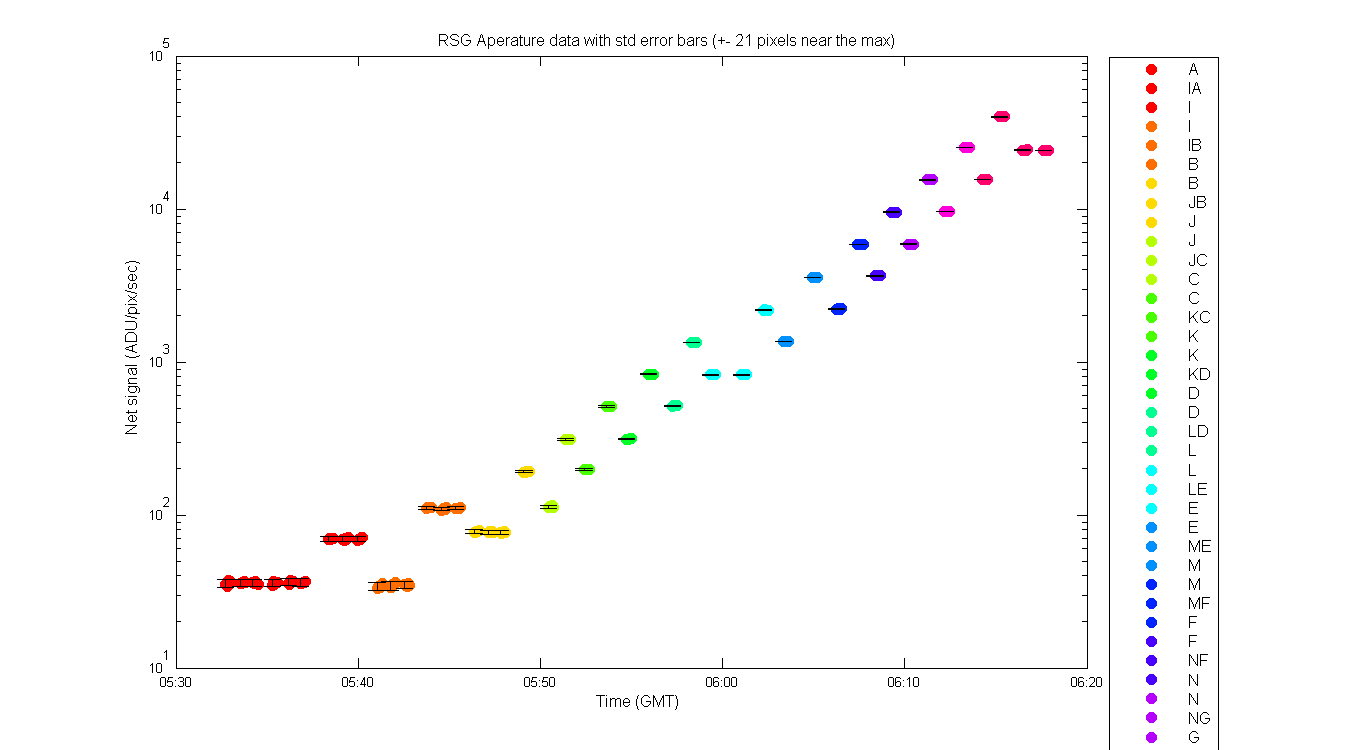
Figure 3
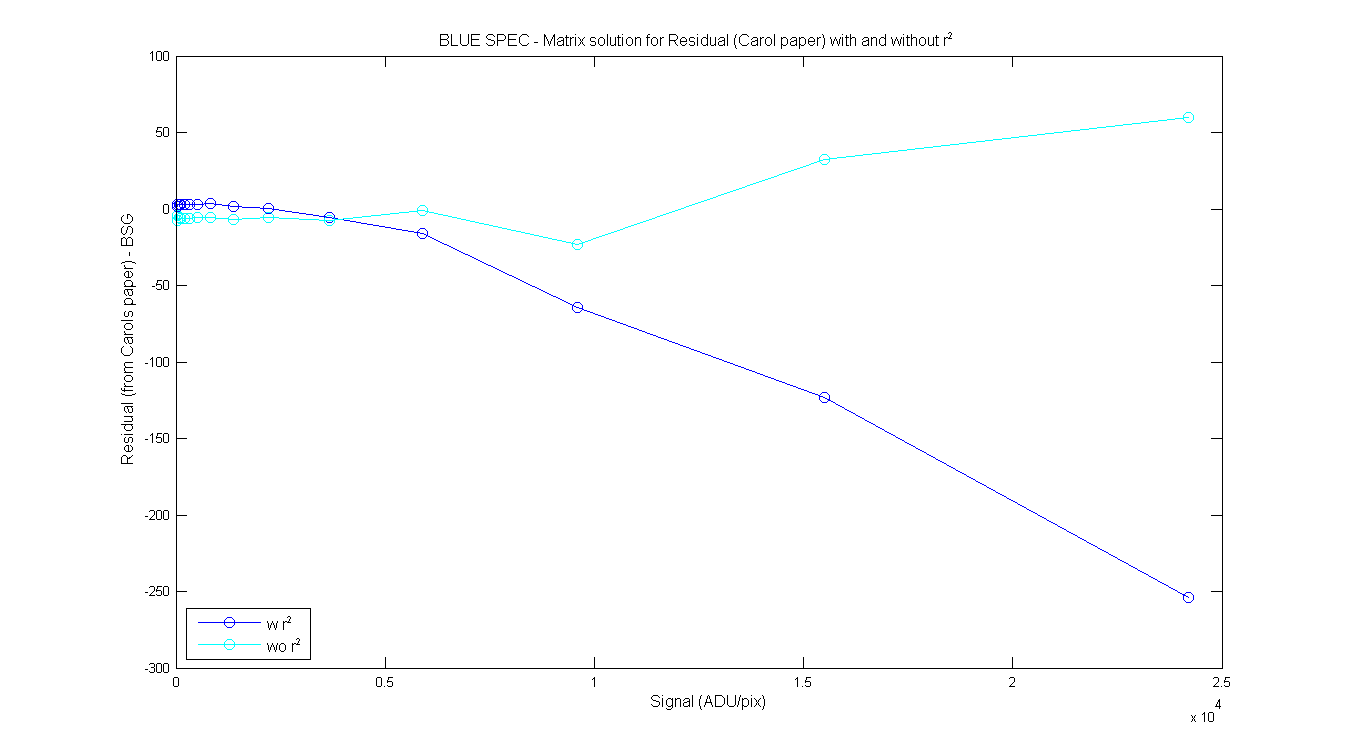
Figure 4
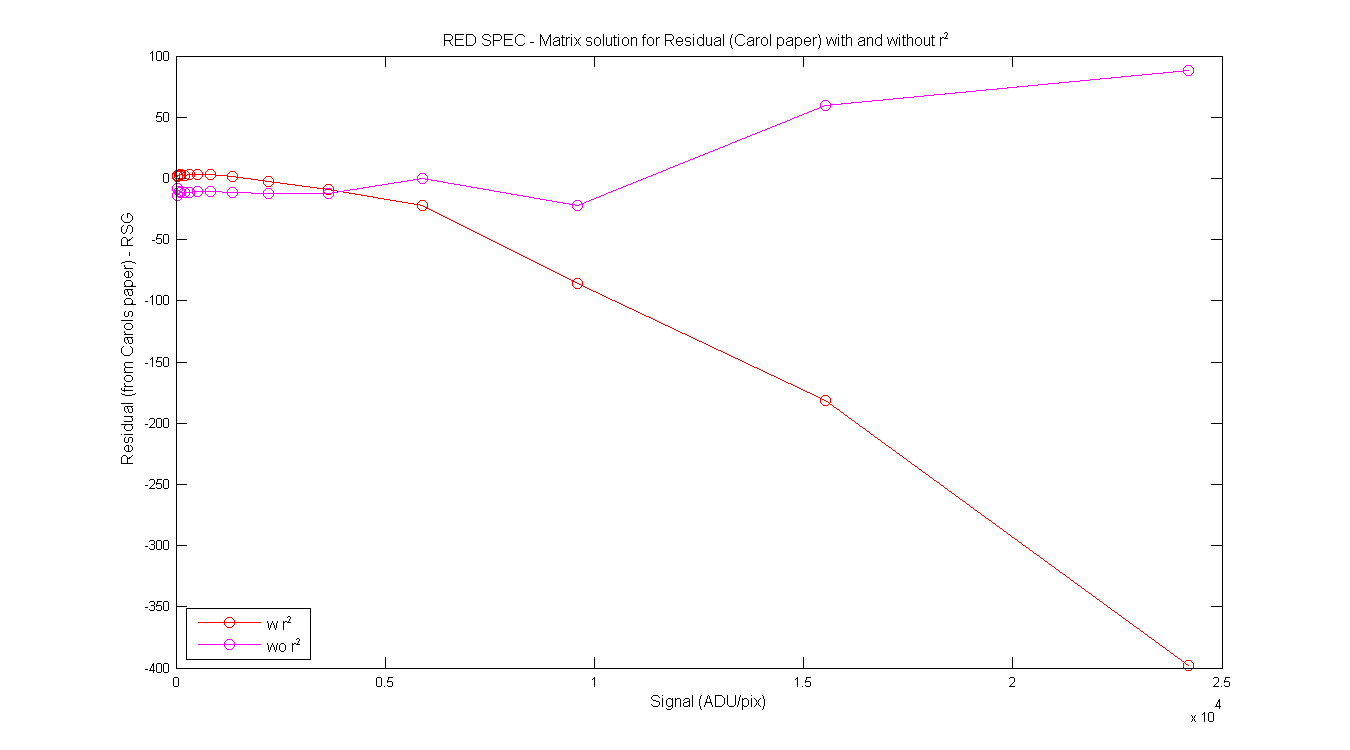
Figure 5
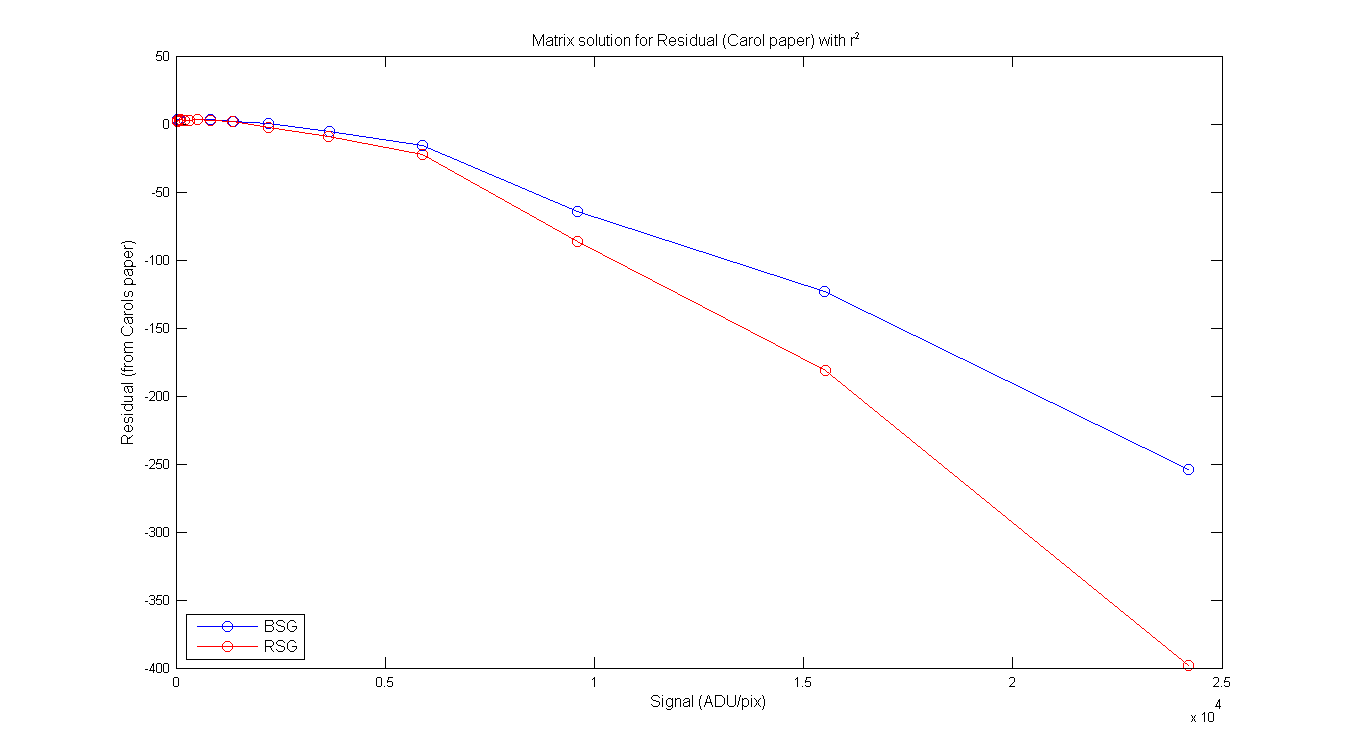
Figure 6
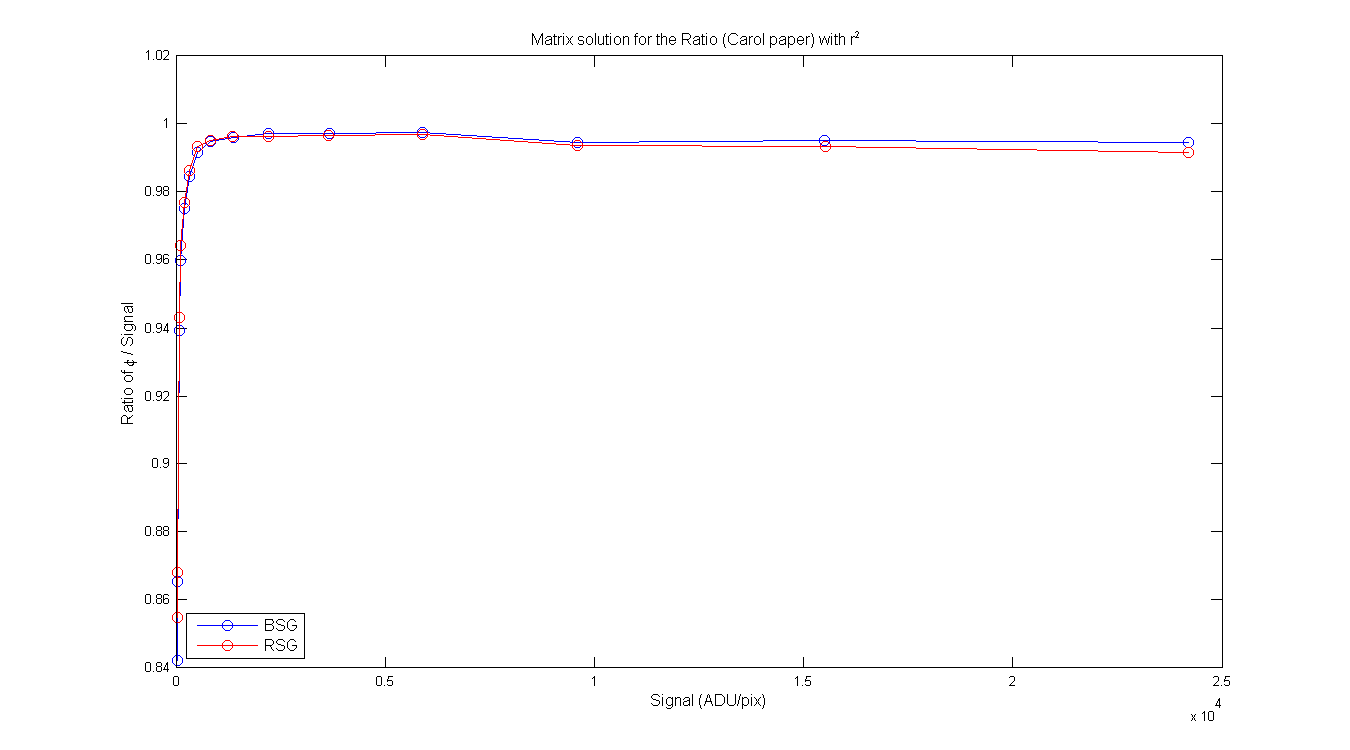
Figure 7
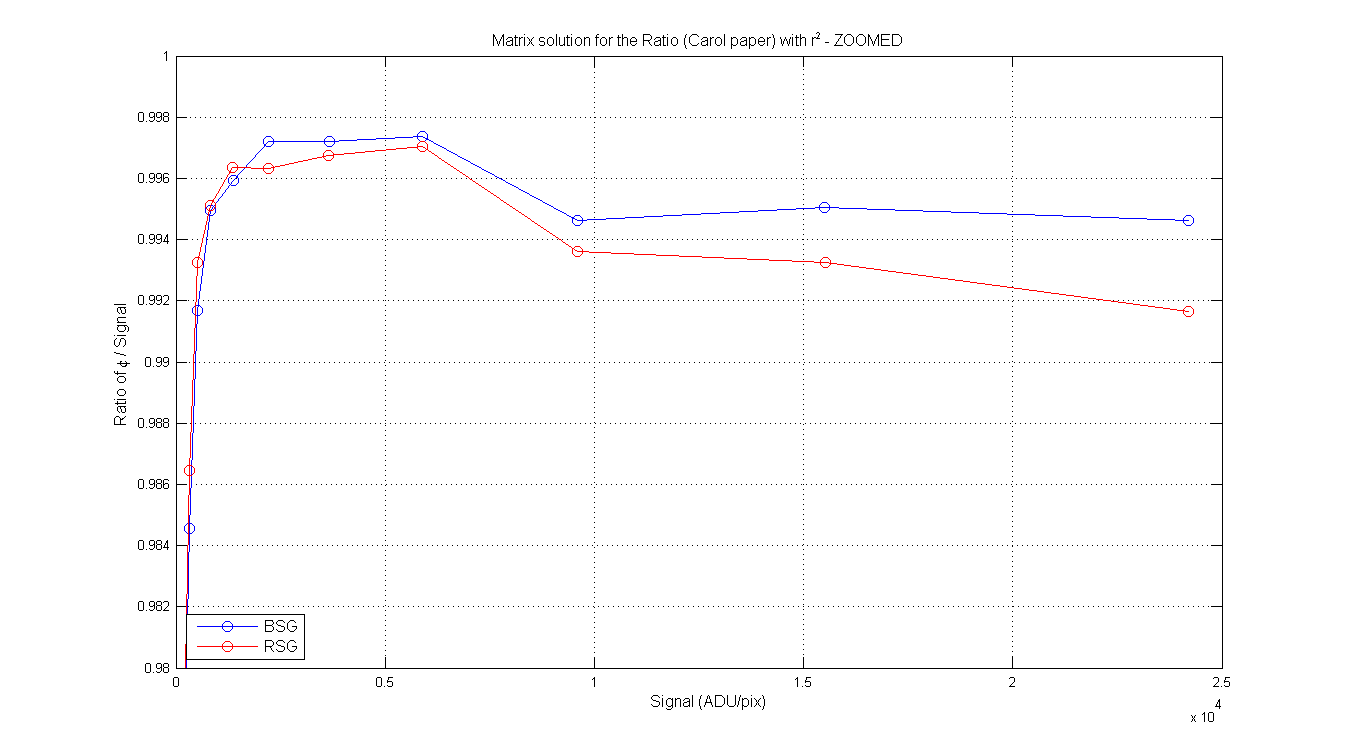
Figure 8
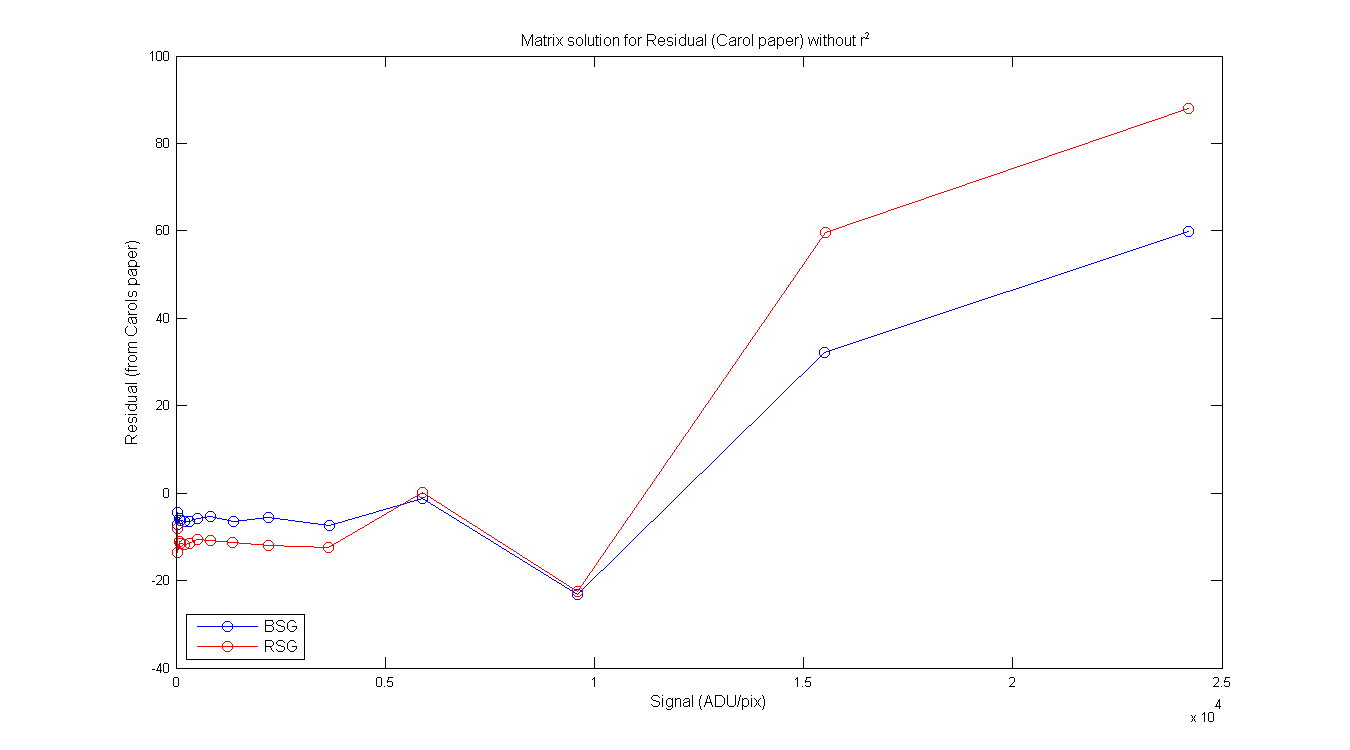
Figure 9
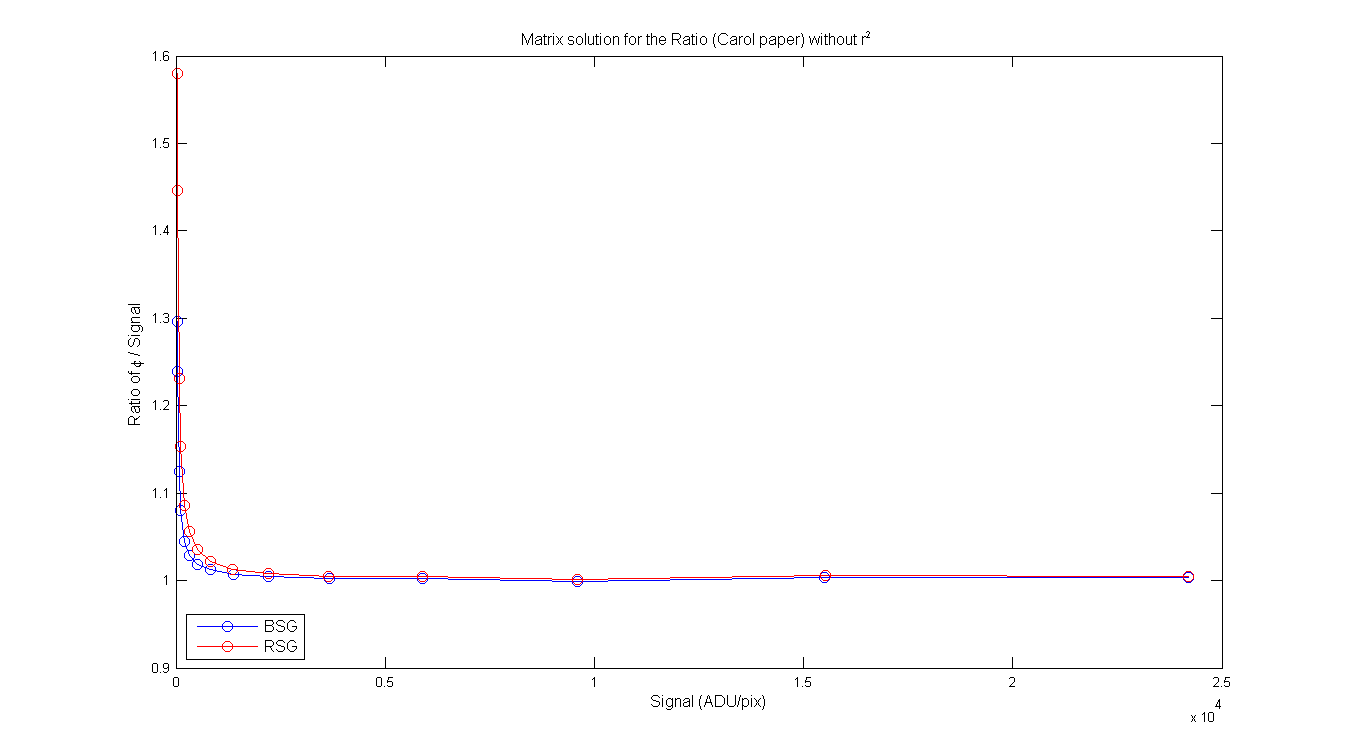
Figure 10